Home Research Quantum Rings Nanotube TransportElectronic Textures Teaching Intro for Majors Grad Stat. Mech. Modern Physics Adv. Solid StatePersonnel Publications Links

Quantum Rings:

Quantum Dots, while interesting, are pretty much the atomic physics of the 1930's: we can look at their shell structure, spin-orbit effects, Stark shift, etc. But what if we could produce systems that have no natural analog?

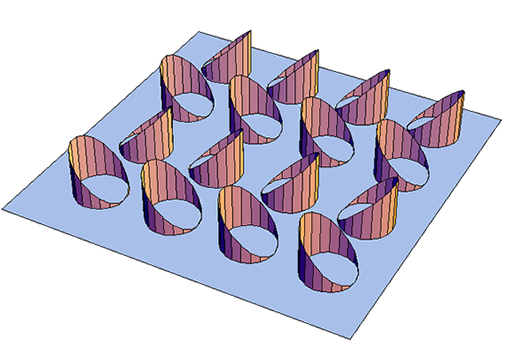
Quantum Rings are one possibility. By confining an electron to a 1D ring we fix the magnitude of its dipole moment, but not its direction. Classically an array of such rings will allign in striped antiferroelectric order (AFE), as shown at the right. That means that the ground state has a four fold degeneracy. If we consider a charge fluid, there is no symmetry breaking: the charge distribution on each ring has an identical shape with a slight oscillation reflecting the lattice. What about a quantum ring?

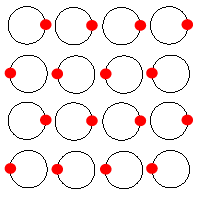
There is a competition between the kinetic energy and interaction terms that can be tuned by geometry, screening, and even an applied magnetic field! The 1D problem exhibits a quantum phase transition at zero temperature. In 2D there is a finite temperature transition to an AFE state, as shown at the left. We can imagine a host of related problems, where we change the charges on each ring or their geometry.

Quantum Spheres, or "quantum well quantum dots" raise similar issues. These are arrays of colloidal nanocrystals in which electrons are confined to a spherical shell. The classical model produces a checkerboard AFE state (not striped). The quantum case is under investigation.

Publications:

• "Polarization transitions in interacting ring 1D arrays," Bahman Roostaei and Kieran J. Mullen, Phys. Rev. B 78, 075411 (2008).