|
||||
|
||||
| Topics: Electric field, Coulomb's law, charge
distribution, vector addition, vector algebra. Pre-requisite skills: Qualitative summation of vectors, Coulomb's law. Approximate completion time: Under an hour. |
||||
Provide sufficient detail to verify that the assignment was completed in a meaningful manner. |
||||
Applet by Physics 1 |
||||
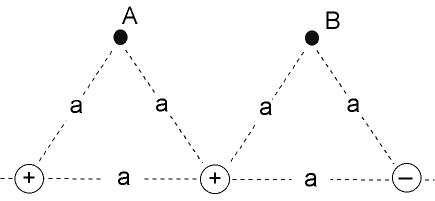
| 1. In the figure below is a layout of
three charges. Each charge has the same value (although obviously not the same
sign) and is separated by a distance a from the other. There are also
two points shown in the figure, point A and point B. Each point is a distance a
from the nearest charge, so that the two nearest charges and the point form an equilateral
triangle.
(Note: In the following questions you may find it convenient to set the value of each charge Q = 1 mC or Q = -1 mC. Assume the distance a is measured in meters.) (a) For each point, draw the electric field vectors due to each of the three charges, then sum the vectors (using either the head-to-tail method or the parallelogram method) to find the resultant electric field. Be sure to scale the length of each electric field vector proportionally with respect to the others. (In other words, a field strength due to one charge that is four times larger than due to another charge should have a vector that is four times longer than the other.) (b) Roughly, in which direction will the electric field point at points A and B? (c) Which point corresponds to a stronger electric field? (d) Using the above applet, place the charges in the applet window in order to mimic the charge distribution in Fig. 1. Does the resultant electric field shown in the applet confirm your results? (Hint: How is the strength of an electric field represented by the plot in the applet?)
4. How would your results change if the negative charge was placed in the middle and the two positive charges were placed on the outside? Explain in terms of symmetry. |
||||
Helpful Resources
|
||||
Return to Web Assignments |
||||