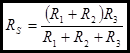Superposition:
Analyzing circuits with multiple sources.

 

Caveat:  Superposition only works for linear circuits. Circuits with R, L, C.

 

The current or voltage at any point in a circuit containing multiple sources (current and/or voltage) is the superposition (sum) of the currents or voltages imposed separately by each source.

 

Procedure for analyzing a circuit using superposition.

 

• Turn on the sources one at a time.
• For each source that is “off”, replace it with its characteristic resistance. (Ideal voltage sources R=0, a short circuit. Ideal current sources R=∞, an open circuit.)
• Analyze for the desired quantity due to each source.
• The full solution for all sources active is the sum of the contributions due to each source individually.
• Carefully observe the signs of the individual voltages and currents. The polarity of the voltages and the direction of the currents may not be the same for all sources.

Example:  Find the Thevenin equivalent voltage, V_TH and the source resistance R_S of the following network as seen at the terminals. Because V_TH is the open circuit voltage, we simply need the voltage at the terminals, V, which is the same as the voltage across R₃.

Because the network has 3 internal sources we will use superposition to solve the problem. Superposition says that V is the sum of the voltages contributed from each of the 3 sources. V = V₁ + V₂ + V₃. We will determine the voltage contribution from each voltage separately by turning on only one source at a time. Sources that are “off” are replaced with their characteristic resistance.

Find V_TH and R_S using superposition.

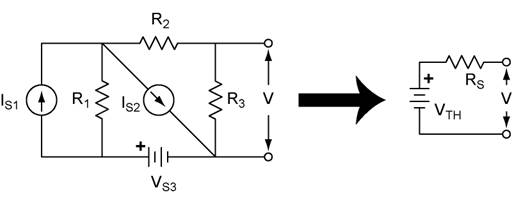
Solving for V₁ due to I_S1.

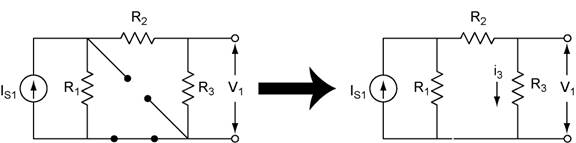
The terminal voltage is the voltage drop across R₃. We also note that R₁ and R₂+R₃ form a current divider. To find V₁ we need i₃ which we can find from the current divider equation.

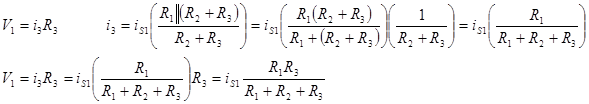
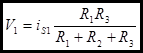
Solving for V₂ due to I_S2.

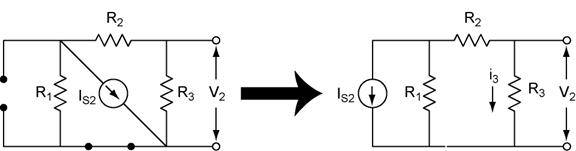
We see that circuit reduces to almost the same problem as for I_S1, except that the direction of the current is opposite. We have chosen to keep the same direction of i₃ to remind us that we need a negative sign. The lower terminal will obviously be more positive that the upper terminal. We must be very careful of the signs!

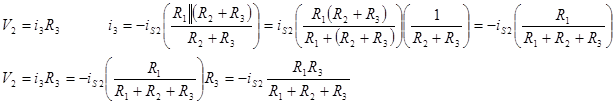
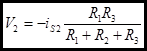
Solving for V₃ due to V_S3.

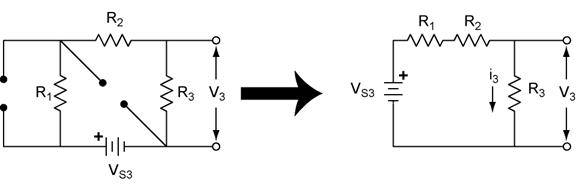
Again, the terminal voltage is the voltage drop across R₃. However we also recognize that R₁+R₂ and R₃ form a voltage divider. To find V₃ we simply use the voltage divider equation.

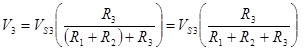
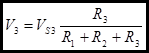
The V_TH of this network as seen at the terminals is the sum of each of these component voltages. Be careful of the signs!!

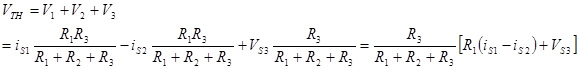
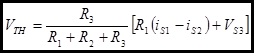
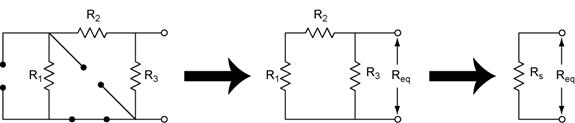
To solve for the source resistance, R_S, we simply turn off ALL of the sources and solve for the equivalent resistance of the resulting resistor network.