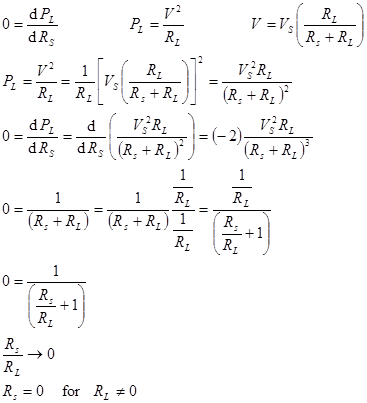Maximum Power Transfer
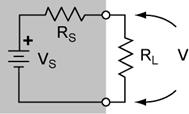
Real power sources include devices such as your audio amplifier. When a load is connected to any power source it is often desired to transfer the maximum power to the load (speakers for example). Because real sources have an internal source resistance, some power is ALWAYS lost within the source. In the example below we have attached a load RL to a voltage source VS with internal resistance RS. This is the load matching problem. The second example is for a ideal power supply where we are simply trying transfer the maximum power to the load.
Maximum power transfer for fixed non zero RS, the load matching problem.
Given a source with an internal resistance RS what value of RL will give the maximum power transferred to RL? Reducing RL increases the current in the circuit, but decreases the voltage across RL. Increasing RL increases the voltage, but decreases the current. Because the power delivered to the load PL is the product of the current and the voltage, there must be a value of RL that maximizes PL.
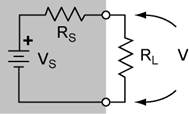
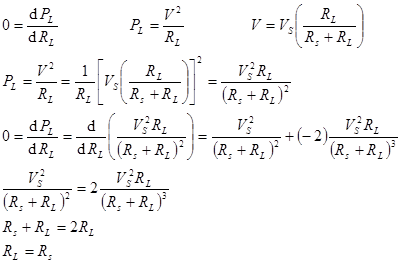
The maximum power transfer occurs when the load resistance equals the source resistance. Audio amplifiers specify the impedance of the speakers; this is precisely the same concept. For example, an amplifier designed to drive an 8 ohm speaker can also drive two 4 ohm speakers placed series or two 16 ohm speaks placed in parallel. Any combination that changes the equivalent load resistance will result in less volume.
Maximum power transfer for fixed non zero RL, the ideal power source problem.
Now let’s consider the case where RL is fixed and RS can be varied. That is, given RL, what RS will maximize the PL? Another way to state the problem is: What value of RS will minimize the PS, power dissipated in the source? Clearly the smaller we make RS, the smaller PS will become. Hence if RS = 0, PS = 0, so all the power from the source is transferred to the load. Therefore the answer is RS = 0. The mathematical proof is below.