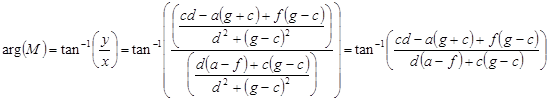Complex Numbers Review

In electronics we use complex numbers as a convenient way to keep track of phase.

In mathematics i = √−1, but in electronics we use j instead of i because i is the current. Thus in this course j = √−1.

In these examples the general complex variable is z. However in electronics Z is impedance, the complex form of R the resistance.

vocabulary

complex variable              z

magnitude of z r

argument of z θ

real part of z x

imaginary part of z y

complex conjugate of z z*

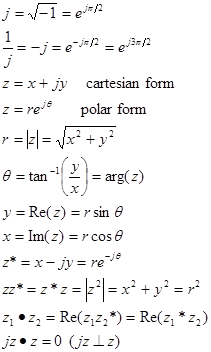
Complex Numbers Practice

Example:

Simplify M, this means

1) collect the terms in the numerator and the denominator to put the expression in the form

2) remove any imaginary components from the denominator by multiplying the numerator and the denominator by the complex conjugate of the denominator,

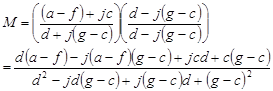
3) Collect the real and imaginary terms and simplify the expression.

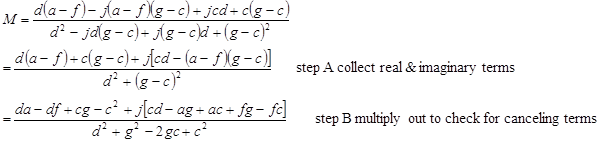
What does simplified mean? That depends on the application. Generally:  1) A simplified expression should have any canceling terms removed; 2) The distributive property should be used to pull out (collect) as many terms as possible. This generally gives the best physical insight in to problem. The best way to make sure an expression is simplified is to: a) multiply it out, b) cancel any terms that can be eliminated, c) collect any terms, which if there was nothing the cancel, reverse step a!

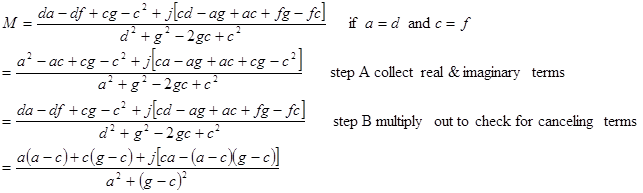
Find Re(M) and Im(M), the real part and the imaginary part of M. To do this you need the have M in the form x + jy. Re(M) = x and Im(M) = y. By simplifying M above you have made this very easy.

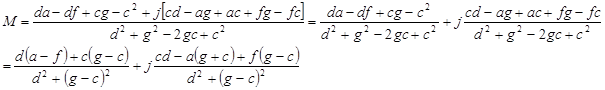
thus

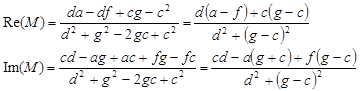
Note that the imaginary part is the coefficient of j and cannot be complex!

Find |M|, the magnitude of M. You have two routes to the solution illustrated by this expression:  r = √(z z*) = √(x² + y²)

1) The first method is to multiply M by its complex conjugate M* and then take the square root.

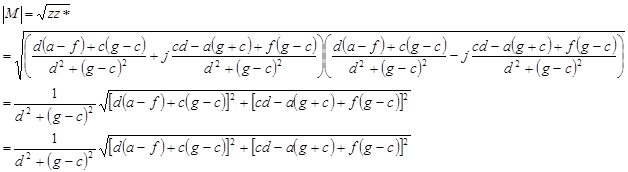
2) The second is to take the square root of the sum of the squares of the real and the imaginary parts.

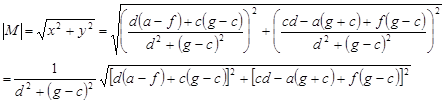
Find arg(M), the argument of M, also known as the phase. This is simply θ = tan⁻¹(y/x), the inverse tangent of the ratio of the imaginary to the real part of M.