Lab 1: Resistor Networks Puzzle
In this lab you will perform DC resistance measurements using your digital multimeter (DMM) as an ohmmeter. You are given a black box with 4 terminals. Inside the box is a resistor network. Your task is to determine the value of the resistors in the network. You can use your DMM, and two shorting wires for your measurements. You are not permitted to open the box. This is considered cheating.
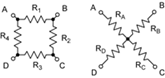
Regardless of how many resistors are present inside the box, how they are interconnected with the terminals, or interconnected with each other, the problem reduces to four resistor values. That is to say that any four-terminal circuit can be represented by four resistors. These resistors can either be connected as a square or as a cross. It is possible to determine which topology you have by measurement.
The actual measurements in the lab will take less time than you will probably need to solve this problem. The trick is to be organized with your measurements so that you do not miss a critical one or mix them up. I know of 31 unique measurements. Hint: Banana cables can be used to connect terminals, thus shunting (shorting out) the resistors in between those terminals.
It should be clear that solving for four unknowns only requires four measurements. Some of the measurements carry redundant information. However because the exercise of this lab is take measurements, you must make all the possible measurements.
Before you can begin analyzing your data, you will need to determine which topology you have.
You will need to justify your strategy in the lab report, i.e. explain what you are doing and why you are taking that approach. Show the circuit analysis and the mathematical steps that lead you to the solution. Present your measurements in a table. (Use a table to organize you results.) If you prove that you have one topology, explain why you think this is the case and justify your answer with an example circuit analysis.
In your lab report be sure to include all of the schematics, derivations of the equations, and all of the calculations. Use significant figures for error propagation. Explicitly answer all the questions posed in the lab.
Conductances. For parallel circuits it can be simpler to use conductances in you equations rather than resistances. For example, the conductance G = 1/R. Therefore for two resistors, R1 and R2 in parallel, R = R1||R2 = [1/R1 + 1/R2]−1 ↔ G = G1+G2. Viewing a parallel resistor problem in this way can greatly simplify the algebra. Note that setting up the problem in terms of conductances is equivalent to simply carrying through the algebra in terms if (1/R)’s.
Your lab report should include:
1. 5pts) One paragraph explaining your reasoning to distinguish a square from a cross geometry.
2. 10pts) Derivation of your solution. This must be algebraic! Show the steps in your derivation leading up to and including the solution.
3. 25pts) Completed table of measurements, including the schematics and shorthand equations for the equivalent resistance. (point breakdown: 5: measurements; 10 schematics ; 10 shorthand REQ)
4. 5pts) The 4 resistor values.
5. 3pts) Test your results (3 checks). Plug results into the equations to verify that you reproduce your actual measurements within experimental error.
6. 2pts) Number of the box.
7. 10 notebook pts) Photocopies of the appropriate pages from your notebook.
