Introduction to Vectors and Vector Algebra


Vectors and Vector Algebra
Why do we bother with vector algebra? Learning vector algebra represents an important step in students' ability to solve problems. The importance of vector algebra can be understood in the context of previous steps in knowledge: At some point (usually in middle school or high school) students are taught basic algebra because the mathematics they have known up to that point, arithmetic, cannot solve most real-world problems. For example, a student may be asked to find the speed required to travel 33 miles in 60 minutes. For this problem, arithmetic alone is not terribly useful. During high school students begin to realize that even algebra cannot solve problems that incorporate two-dimensional space, so they learn trigonometry and geometry. For example, if a student was trying find the amount of concrete needed to fill a cone-shaped hole, simple algebra alone will be of little help. However, geometry and trigonometry are very difficult to apply in many situations. Vector algebra was invented in order to solve two-dimensional and three-dimensional problems without the use of cumbersome geometry. Although it is possible to use ordinary trigonometry and geometry to solve most of the physics problems you are likely to encounter, vector algebra has some significant advantages: Vector algebra is much easier to apply than geometry and requires knowledge of fewer rules. The mechanics of vector algebra are straightforward, requiring less intuition and cleverness in finding a solution. (Remember those nasty geometry proofs from high school?) Vector algebra operations are much easier to express with familiar nomenclature. (For example, the statement C = A + B is a typical vector algebra expression.) Many of the rules learned in basic algebra also apply in vector algebra. (For example, you can add the same vector to both sides of an equation, you can divide both sides of an equation by a number, and so on.)
What is a vector? Suppose you were given the job as weatherman for your local television station. You would like to convey to your audience the wind speeds and directions in their area, and how they compare to other areas. First you could try writing down the speed and direction of the wind at various locations on a map. However, notice that the viewer is going to have a miserable time. First, he will need very good eyesight, and patience. Most importantly, such a system is insufficient for detecting general trends in wind directiona and speed. To do so, the viewer has to write down all of the data for each location and study it -- not a good system!
A Slight Improvement Another idea is to indicate the direction of the wind with an arrow, while writing the wind speed next to the arrow. Now the viewer can compare the directions of the wind easily with other locations. Some of the arrows may correspond to mere breezes, others to full-blown gales. Therefore, such a system is visually misleading, because numbers alone do not provide the necessary visual cues to establish general trends in wind speed.
Using the Idea of the Vector Is there a way that we can incorporate both aspects of wind, speed and direction, with a simple system? Yes! Make the length of the arrow correspond to the speed of the wind. With this system, long arrows correspond to high winds, and so on. Now, the viewer can tell which direction the wind is blowing in his area with a quick glance. Furthermore, the viewer can tell how the wind speed in his area compares other areas. 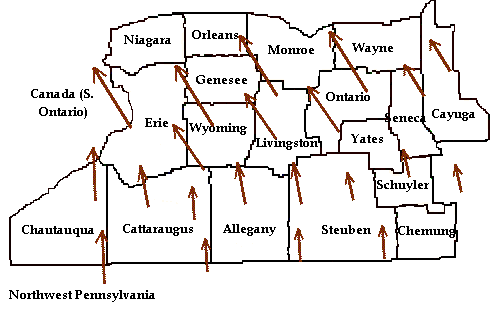Once the arrow indicates both a magnitude of some sort (in this case, the speed of the wind) and a direction, it is called a vector. The vector in this example is a velocity vector. The length of the arrow, which represents the magnitude of the velocity, is called the speed. Notice that speed and velocity are not synonyms in physics -- the term velocity refers to a vector quantity and has both a magnitude (the speed) and direction. Notice that if the viewer wants to know exactly how strong the wind is in a particluar location he will still have to refer to numerical data -- the length of the vector arrow is not sufficiently precise to provide this information. So at this point, we would guess that vectors have very limited quantitative use. But we would be wrong.