The Component Method, Part 1 |
|||||||||
The Basics - Good Vectors from Bad The component method of summing vectors is universally feared by introductory physics students, but is actually simple as long as you don't get too worried about trigonometric details. The foundation of the component method actually relies on a basic principle: Vectors are easy to sum if they fall into two categories:
To fully appreciate the importance of these two principles, complete the following web assignment. |
|||||||||
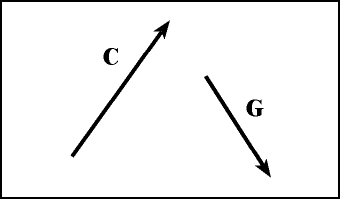
What are component vectors? Consider the equation vector C = A + B, which simply states that "vector C is the sum of vectors A and B." This statement is an equality, which is a very strong statement -- it means that C can be replaced with the term A + B whenever we see fit. We will take advantage of this property to greatly simplify vector addition by replacing vectors that are hard to sum (we will call them bad vectors) with vectors that are easy to sum (good vectors). Now there are any number of vectors that sum to vector C, but we are going to choose A and B very carefully. Consider the following example, where we are trying to add the two vectors C and G. If you checked out the previous web assignment above you would appreciate how difficult it is to add these two vectors because they do not point along the same direction, nor are they perpendicular. Therefore, we consider them bad vectors.
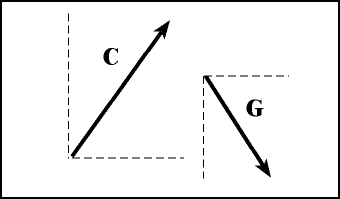
But why not replace both bad vectors with good vectors that are easy to sum? In the figure below, we have defined two directions with dashed lines we call the x-direction (horizontal) and y-direction (vertical). If we can somehow find replacement vectors for C and G that line up along these directions, then we will be guaranteed that all vectors will either be pointing along the same direction or perpendicular to each other.
But how do we find these good vectors? |
|||||||||
|
Applet by Zona Land |
|||||||||
In the applet above, we have isolated vector C (in black). Notice that vectors A and B (the red and blue vectors) point along the x-direction or y-direction and that they both sum to C. Now using the mouse, drag vector C around and watch what happens to A and B. Notice that no matter which direction C is pointing, vectors A and B always form a perfect rectangle. In the figure below, we have replaced both vectors C and G with their component vectors. We can erase vectors C and G if we wish-- they are no longer needed. We now have four vectors instead of two, but each of these four vectors is guaranteed to be either parallel or perpendicular to the others.
We now have four vectors instead of two (see the figure below), but each of these four vectors is guaranteed to be either parallel or perpendicular to the others.
Using our basic rules listed above, we can guess that we have now simplified the problem a great deal. And we have. |
|||||||||
| A Little Bit of Trig (and I
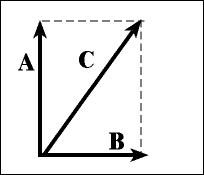
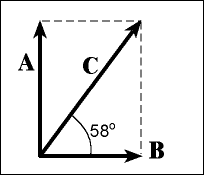
Mean Little) Now that we know we have to replace C with A and B, how do we find the lengths of A and B? (We already know their directions, right?) To find these lengths is simple, and requires nothing more than the ability to punch the "COS" and "SIN" buttons on your calculator. But what are COS and SIN? Notice in the applet above that vectors A and B are always shorter than C. The COS and SIN buttons simply take the length and direction of C and use this information to find the lengths of A and B. In the figure below we examine our earlier example, defining a direction of C of 58 degrees with respect to the x-direction (horizontal).
But which do I choose? COS or SIN? The rule here is simple: Do you see the angle symbol that we have drawn in the figure? Well, if that angle sign touches the component vector for which you are trying to find its length, use COS. If the angle sign touches, it's COS! If you use COS on one component vector, use SIN for the other. In summary, COS and SIN are "shrink factors" -- the amount of shrinkage depends on the angle. So in our example above, the length of vector B is given by C X COS(58). The reason? The angle symbol touches vector B, so we use the COS button. Since we used COS for B, we use SIN for A. In summary, B = C X COS(58), A = C X SIN(58).
Suppose that the length of vector C was 60 (in whatever units). Then, B = 60 X COS(58) = 60 X 0.53 = 32, A = 17 X SIN(58) = 60 X 0.85 = 51.
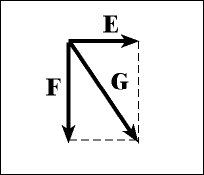
According to these calculations, vector A should be longer than vector B, and nearly as long as the original vector C. And vector B should be just slightly longer than half of vector C. Looking at the figure above, this appears to be the case. (You can use the above applet to verify these results as well, although it requires some precise movement of the mouse.) So all the trigonometry you are going to need at this point consists solely of finding the angle symbol, seeing which component vector it touches, and using the COS button to find the length of that vector. Use the SIN button for the other and voila, you have successfully broken the original vector into its componenent vectors. Naturally, you would then do the same for vector G. Before moving on, test your ability to break a vector into its components. |
|||||||||
  |
|||||||||