
|
 |

|
|
|
| Topics: Vector algebra, vector addition, vector
subtraction, net force, Newton's Second Law, blocks on planes, normal force. Pre-requisite
skills: Understanding of Newton's Second Law.
Approximate completion time: 30 minutes. |
Provide
sufficient detail to verify that the assignment was completed in a meaningful manner.
|
|
Applet by Walter Fendt |
A. One advantage of Walter Fendt's Using Vectors page
is that you can add up to four vectors.
- Go to this site, and on the graph select "4" for "Number of
Vectors." Now using the mouse drag out three vectors of arbitrary length
and direction. Now drag out the fourth vector that you think will cause all four to
add to 0. Watch what happens when you click on the "Add Vectors" button
and describe.
- What method is the applet using to add the vectors? In comparison to the average
lengths of the original four vectors, is the length of your resultant vector reasonably
small?
- Using the mouse, grab one of the vectors and drag its head around on the page.
Pretty cool, heh? Can you force the resultant vector to be 0?
|
| B. In attempting to solve the classic block-on-a-plane
problem, a student has drawn the following forces on the block. One of these vectors
(pointing straight down) represents the force of gravity acting on the block. The
other (pointing up the ramp) represents the frictional force. 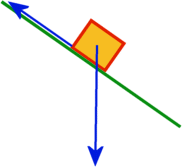
- Using the above applet, draw the vectors shown and sum them by pressing the
"Resultant" vector. In which direction is the resultant vector?
- In which direction will the block accelerate, and why?
- Which force is missing? If you were to draw this force on the applet such as to
create an acceleration that points down the inclined plane,describe how you could judge
the length of this force vector fairly accurately. (Hint: What should the
value of the acceleration be perpendicular to the plane?)
- Suppose the vector pointing downward (which, again, represents the force of gravity
vector) has a magnitude of 10 N. What is (roughly) the magnitude and direction of
this missing vector?
|
C. Now we are going to investigate the relationship
between the force of friction and the normal force. Specifically, we are going
to use the above applet to draw three vectors that represent (1) the force of gravity, (2)
the force of friction, and (3) the normal force acting on the body placed on an inclined
plane.
- Using the above applet, draw the three vectors and sum them by pressing the
"Resultant" button.
- Assume the block in this problem accelerates. In which direction should the
resultant vector point to make physical sense?
- Unless you were very fortunate, your resultant vector probably does not point in the
right direction. Remedy this situation by using the mouse to modify the lengths of
the three forces. (The frictional force vector is probably too long, for starts.)
- Now using the mouse, increase the length of the frictional force vector. Can the
resultant vector be made to point in the opposite direction as to Question C3?
Does this make sense physically?
- Discuss why the equal sign in F = mN is not strictly
correct. What should be the correct relationship?
|
Helpful Resources
- Vector Addition
and Subtraction by Wesley Dean.
- Vectors and
Motion in Two Dimensions by Tom Henderson.
- Vector
Illuminations by Ron Greene.
- Sum
of Vectors by Phillip Dukes. (Assignment)
- Vector
Math Worksheet by Gary Richert (Assignment)
- Vectors by
Angel Franco Garcia. (in Spanish)
- Zona Land's
Vectors by Ed Zobel.
|
Return
to Web Assignments |





